The conservation of energy is a fundamental principle in physics that states that the total energy of an isolated system remains constant over time. In other words, energy cannot be created or destroyed; it can only change forms or be transferred from one part of the system to another. This principle is derived from the law of conservation of energy and is a fundamental concept in classical mechanics and other branches of physics.
Total Mechanical Energy
In classical mechanics, the total mechanical energy of a system is the sum of its kinetic energy (associated with motion) and its potential energy (associated with the position or configuration of objects). Mathematically, this can be expressed as:
Total Mechanical Energy = Kinetic Energy + Potential Energy
E_total = KE + PE
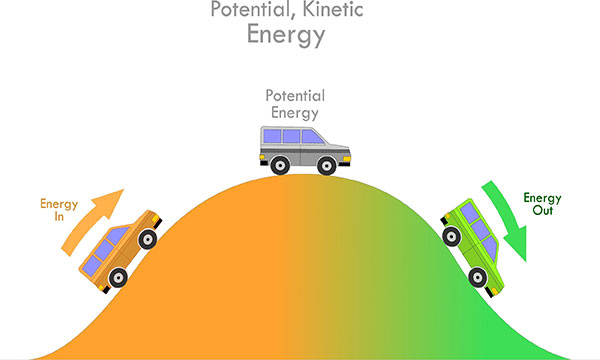
Kinetic Energy (KE)
Kinetic energy is the energy of an object in motion. It depends on the object's mass (m) and its velocity (v) and is given by the formula:
KE = (1/2)mv^2
Kinetic energy is directly proportional to the square of the object's velocity.
Potential Energy (PE)
Potential energy is the stored energy that an object has due to its position or configuration within a force field. There are different types of potential energy, including gravitational potential energy and elastic potential energy. Gravitational potential energy near the surface of the Earth is given by the formula:
PE = mgh
Where:
- PE is potential energy
- m is the mass of the object
- g is the acceleration due to gravity
- h is the height above a reference point
Elastic potential energy is associated with the deformation of an elastic material, such as a spring, and is given by:
PE = (1/2)kx^2
Where:
- PE is potential energy
- k is the spring constant
- x is the amount of deformation (displacement from equilibrium position)
Conservation of Mechanical Energy
In the absence of external forces (like friction or air resistance), the total mechanical energy of an isolated system remains constant. This principle is often used to analyze the motion of objects, such as projectiles, roller coasters, and pendulums, where mechanical energy is conserved.
Non-Mechanical Energy
While mechanical energy is conserved in many physical systems, it's important to note that energy can also exist in other forms, such as thermal energy, electrical energy, chemical energy, and more. The conservation of energy applies to these forms as well, with the total energy in a closed system remaining constant.
First Law of Thermodynamics
In the context of thermodynamics, the conservation of energy is expressed through the first law, which states that the change in internal energy of a closed system is equal to the heat added to the system minus the work done by the system on its surroundings. Mathematically, it can be written as:
ΔU = Q - W
Where:
- ΔU is the change in internal energy
- Q is the heat added to the system
- W is the work done by the system
The conservation of energy is a fundamental principle that underlies many physical phenomena and is essential for understanding and solving problems in physics, engineering, and various scientific disciplines. It allows us to predict and analyze the behavior of systems and understand the interconversion of energy between different forms.
